When I was working for a small wind turbine manufacturer I was asked to calculate the number of hours per year the houses in the neighborhood of our prototype wind farm would be exposed to shadow flicker from our wind turbine. Now, there are software that calculates this sort of thing with a few clicks of the mouse (the dominant code beeing WindPro). However, these programs cost money, and they are no fun. Instead I solved the problem myself. And to do that I first had to immerse myself in the theory of sundials.

First consider a flagpole casting a shadow on a flat field. There are only a few parameters that influence where the tip of the shadow will be at a particular time. There are some astronomical parameters, namely: the earth axial tilt, the earth rotational speed, the length of the solar year, the eccentricity of the orbital ellipse, and the angle between the major axis of the orbital ellipse and the line of solstices.

Then there are some parameters of the site: height of pole, latitude and longitude. And there is a convention where the year is said to begin relating to the winter solstice.

The rest is a matter of geometry really. Basically one must keep track of exactly how earth is facing the sun at any particular instant in time.

Coordinate tranformations

This is how I think about it. I want to find a transformation from geographic coordinates (which rotate with earth) to a coordinate system with origo in the center of the earth that always has the sun in the direction of the y-axis and the z-axis normal to the orbital plane. In this system it should be easy to find the tip of the shadow by finding the intersection between the line passing from the sun, through the tip of the pole and the sphere that is earth. Once this is done we go back to geographic coordinates by applying the inverse tranformation.

To implement this we first want a coordinate transformation from the geographic coordinate system (longitude $\phi$, latitude $\delta$, height $h$) rotating with earth to a cartesian system rotating with earth. This is a simple adaption of the spherical coordinate transformation. The only difference being that the latitude replaces the normal angle from the north pole.

$$ \begin{array}{rcl} x & = & (R+h) \sin(\pi/2-\delta)\cos \phi \ y & = & (R+h) \sin(\pi/2-\delta)\sin \phi \ z & = & (R+h) \cos (\pi/2 - \delta) \ \end{array} $$

What we want to do next is to transform a point expressed this way to a nonrotating coordinate system. The transformation matrix for rotation about the z-axis is

$$ R_z(\Omega t) = \left(\begin{array}{ccc} \cos \Omega t & -\sin \Omega t & 0 \ \sin \Omega t & \cos \Omega t & 0 \ 0 & 0 & 1 \end{array}\right) $$

where $\Omega$ is the rotational speed of earth $2 \pi / 86164.09890369 $ rad/s.

Next we want to express this in a system aliged with the earth orbital plane. Thus we want to rotate about the universal y-axis by the axial tilt angle $\alpha = 23.4{}^\circ$. The transformation matrix for this rotation is

$$ R_x(\alpha) = \left(\begin{array}{ccc} 1 & 0 & 0 \ 0 & \cos \alpha & - \sin \alpha \ 0 & \sin \alpha & \cos \alpha \end{array} \right) $$

Finally we want to rotate this system so we face the sun.

$$ R_z(-\theta(t)) = \left( \begin{array}{ccc} \cos \theta(t) & \sin \theta(t) & 0 \ -\sin \theta(t) & \cos \theta(t) & 0 \ 0 & 0 & 1 \end{array} \right) $$

where $\theta(t)$ is the orbital angle. This is a function that must be computed based on orbital mechanics.

The total transformation from ($\phi$,$\delta$) is thus

$$ \left(\begin{array}{c} X \ Y \ Z \end{array}\right) = T(\phi,\delta) = R_z(-\theta(t)) R_x(\alpha) R_z(\Omega t) \left(\begin{array}{c} (R+h) \sin(\pi/2-\delta)\cos \phi \ (R+h) \sin(\pi/2-\delta)\sin \phi \ (R+h) \cos (\pi/2 - \delta) \end{array}\right) $$

The inverse of this tranformation is obtained by

$$ \begin{array}{rcl} h & = & \sqrt{x^2+y^2+z^2}-R \ \phi & = & \mbox{arctan}\left(\frac{y}{x}\right) \ \delta & = & \pi/2 - \mbox{arccos}\left(\frac{z}{r}\right) \end{array} $$

where $$(x,y,z)$$ is obtained by inversing the rotations

$$ \left(\begin{array}{c} x \ y \ z \end{array}\right) = \left(R_z(-\theta(t)) R_x(\alpha) R_z(\Omega t)\right)^{-1} \left(\begin{array}{c} X \ Y \ Z \end{array}\right) $$

Intersection between ray and earth surface

Assume the earth surface is a perfect sphere centered in origo. Also assume all light rays from the sun are coming in the -Y-direction. Now consider a point $\vec{p}$ representing the location of the flagpole tip. The tip may or may not cast a shadow on earth.

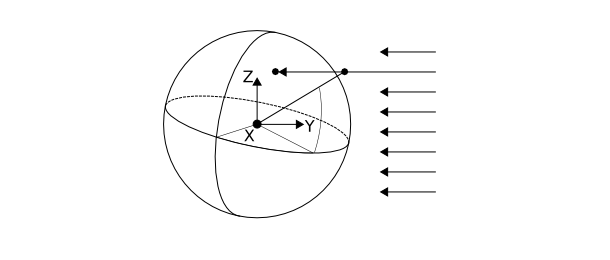
To find the location of the shadow simply apply the formula for line sphere intersection

$$ \ d = -\hat{Y} \cdot \vec{p} - \sqrt{\left(-\hat{Y} \cdot \vec{p}\right)^2-\vec{p} \cdot \vec{p}+R^2} $$

where $R$ is the earth radius and $d$ is the distance from $\vec{p}$ to the intersection. $\hat{Y}$ is a unit vector in the Y-direction. If $d$ is real and greater than zero the location of the shadow is

$$ \vec{s} = \vec{p} - d \hat{Y}. $$

I have implemented this theory as a python module. The source is over at gitHub

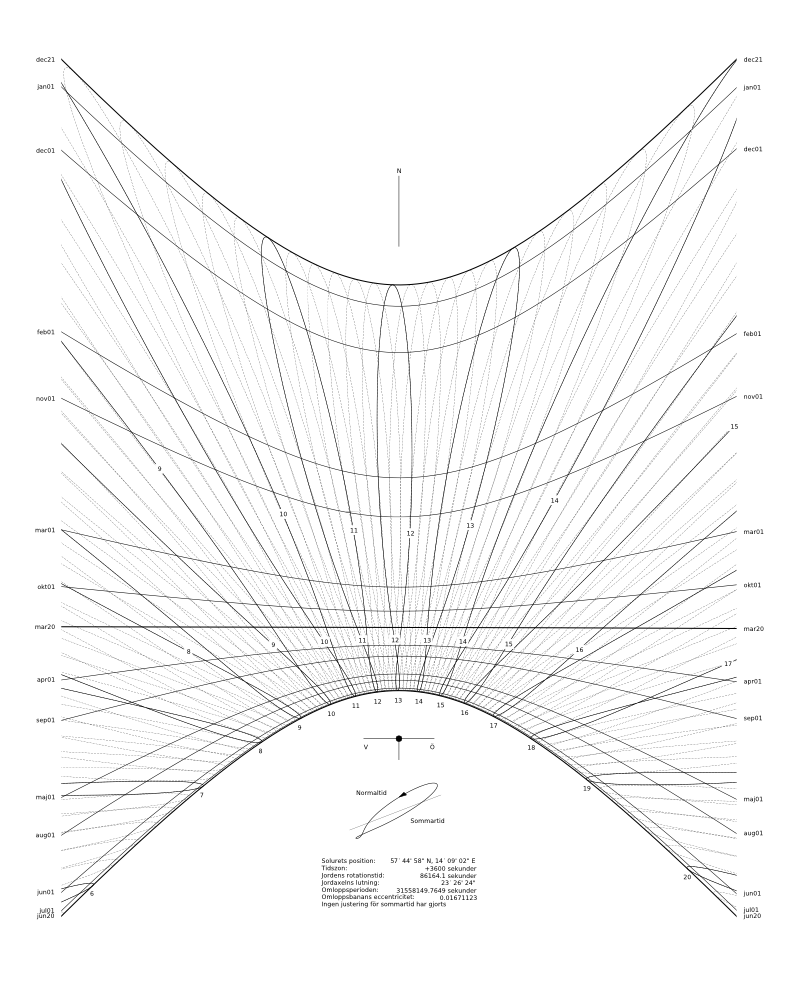
A sundial for my back yard

As an application of this theory I have decided to construct a sundial custom made for my backyard. This is a bit of a project of its own and I will delay the details for a later blog. The following picture is what I have come up with so far. This sundial shows approximate date and also takes daylight saving into account.